【Pythonでテクニカル分析】ボリンジャーバンドを計算して視覚化する方法を解説

記事内に広告を含みます

この記事には広告を含む場合があります。

記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。

株式や為替、仮想通貨など、様々な金融市場でトレードを行う際に欠かせないのが、適切な分析ツールです。トレード分析において、ボリンジャーバンドは非常に人気のあるインジケーターの一つです。

トレンドの変化を視覚的に捉え、売買のタイミングを判断するために役立つので、初心者からベテランまで幅広く活用されています。

この記事では、Pythonを使ってボリンジャーバンドを計算し、視覚的に理解しやすいグラフで表示する方法を解説します。

データを分析してトレンドを見極めたい方や、自分でトレードの戦略を構築したい方にとって、基本的なテクニカル分析手法として押さえておきたい内容です。

ボリンジャーバンドとは
ボリンジャーバンドの使い方
1. スクイーズからエクスパンションを狙う順張りトレード
2. スクイーズを利用した逆張りトレード
ボリンジャーバンドの計算方法
PythonでRSIを計算するコード
ポイントの解説
おわりに

目次へ

ボリンジャーバンドとは

ボリンジャーバンドとは、米国の投資家ジョン・ボリンジャーが開発したトレンド系インジケーターです。移動平均線を中心にその上下に価格の変動範囲（バンド）を描きます。

価格の過熱感や反転の可能性を判断するのに役立ち、相場のトレンドや価格のばらつきを視覚的に確認できる優れたツールです。

まず、ボリンジャーバンドの基本的な構成要素について理解しておきましょう。ボリンジャーバンドは、以下の3つの線（バンド）で構成されます。

中央の線（移動平均線）：通常、20期間の単純移動平均線（SMA）を使います。
上部バンド（+2σライン）：中央の移動平均線に「標準偏差」を2倍加えたライン。
下部バンド（-2σライン）：中央の移動平均線から「標準偏差」を2倍引いたライン。

ボリンジャーバンドの使い方

バンドの幅は価格のボラティリティ（変動率）を反映します。幅が広がるとボラティリティが高く、狭まると低いことを示します。統計学的に、価格が±2σのバンド内に収まる確率は約95.4%です。

ボリンジャーバンドの形状によって、トレンドの変化や継続を予測することができます。主に4つの特徴的な形状があり、それぞれが異なる市場状況を示唆します。

スクイーズ：バンド幅が収束した状態で、ボラティリティが低く、もみ合い相場を示します。エクスパンションの前兆とも言えます。
エクスパンション：スクイーズからバンド幅が拡大していく状態で、ボラティリティが高まりトレンドが発生する可能性を示しますン。
ボージ：エクスパンション後、バンド幅が最大に拡大した状態で、トレンド反転の可能性が高まります。
バンドウォーク：トレンドが継続している状態で、上昇トレンドでは価格が+2σに沿って、下降トレンドでは-2σに沿って推移します。この状態が続く限り、トレンドの続伸が期待できます。

ボリンジャーバンドは一般的に逆張りのシグナルとして使用されますが、開発者であるジョン・ボリンジャーは順張りを推奨しています。

スクイーズからエクスパンションを狙う順張りトレード

スクイーズ（バンド幅が狭い状態）からエクスパンション（バンド幅が広がる状態）への移行を確認します。価格が±2σのラインを超えたら、その方向にエントリーします。

そこからバンドウォークが発生すると、より強いトレンドが発生していると判断できるので、ポジションを保有し続けることで利益の拡大に期待が持てます。

ポジション決済は、トレンド転換のサインであるボージが確認できたら行います。

スクイーズを利用した逆張りトレード

ボリンジャーバンドがスクイーズ状態になっているときは、レンジ相場であると言えます。

ボリンジャーバンドでは±2σバンド内に価格が収まる確率は統計学的に約95.4％と高いので、±2σバンド付近で価格が反発する可能性が高くなります。価格が±2σバンドにタッチしたときに逆張りでエントリーをします。

ポジション決済は、中央の移動平均線にタッチするか、反対の2σバンドタッチで行います。

ボリンジャーバンドの計算方法

ボリンジャーバンドの計算式は以下の通りです。一定期間（一般的には20期間の価格データ）をnとします。

ミドルバンド（単純移動平均）:
\begin{eqnarray} SMA =n SMA \end{eqnarray}
標準偏差：
\begin{eqnarray} σ = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i – \mu)^2} \end{eqnarray}
ここで、n はデータ数、xiは各データの終値、μはデータの平均値です。
±1σ：
単純移動平均±標準偏差
±2σ：
単純移動平均±標準偏差×2
±3σ：
単純移動平均±標準偏差×3

PythonでRSIを計算するコード

RSIを計算しグラフで表示するには、以下のライブラリを使用します。

pandas: 時系列データを処理するためのライブラリ。
yfinance: 価格データを取得するためのライブラリ。
mplfinance: グラフの描画に使用します。

以下のコードを使って、ボリンジャーバンドの計算とグラフの表示をします。使用するデータは、2024年の日経平均株価です。

Python

import pandas as pd
import yfinance as yf
import mplfinance as mpf

# 期間の設定
period = 20

# 株価データを取得（例：日経平均株価のデータを使用）
ticker = '^N225'
data = yf.download(ticker, start='2024-01-01', end='2024-12-31')

# ボリンジャーバンドの計算
sma = data['Close'].rolling(period).mean()  # 移動平均
std = data['Close'].rolling(period).std()  # 標準偏差
upper_band = sma + (std * 2)  # 上部バンド
lower_band = sma - (std * 2)  # 下部バンド

# ボリンジャーバンドを追加してプロット
apds = [
    mpf.make_addplot(sma, color='blue'),
    mpf.make_addplot(upper_band, color='orange'),
    mpf.make_addplot(lower_band, color='orange')
]

mpf.plot(
    data,
    type='candle',  # ローソク足チャート
    addplot=apds,
    style='yahoo',
    title='Stock Price with Bollinger Bands',
    ylabel='Price',
    volume=False
)

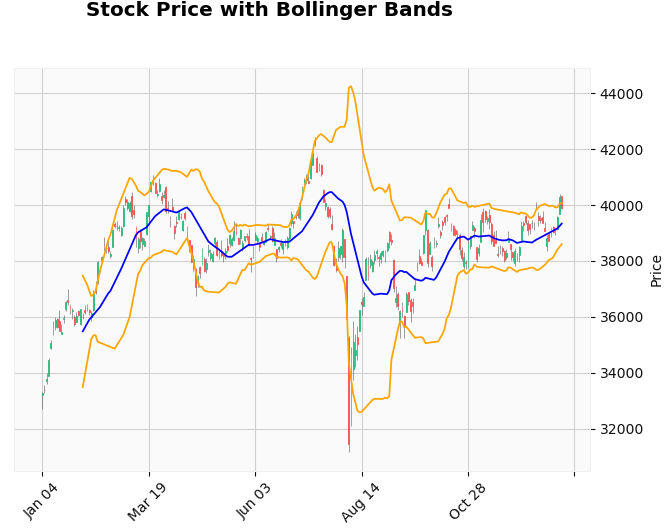
上記のコードを実行すると、以下のようにローソク足とボリンジャーバンドのグラフが出力されます。

ポイントの解説

Python

# 期間の設定
period = 20

periodでボリンジャーバンドの期間を設定します。通常は20期間ですが、変更したい場合はこの数値を変更してください。

Python

sma = data['Close'].rolling(period).mean()  # 移動平均
std = data['Close'].rolling(period).std()  # 標準偏差
upper_band = sma + (std * 2)  # 上部バンド
lower_band = sma - (std * 2)  # 下部バンド