この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
SBI証券や楽天証券の銘柄を探す機能のひとつに、チャート形状銘柄検索ツールというものがあります。
これは、日足チャートの形状を9パターンまたは25パターンに分類し、同じ傾向の銘柄を探すことができるツールです。例えば、日経225の銘柄から上昇基調の銘柄を絞り込む事ができます。
本記事では、Pythonで相関係数を基に、チャート形状銘柄検索ツールの作成方法について解説します。
チャート形状銘柄検索ツールとは
チャート形状銘柄検索ツールとは、日足チャートの形状を9パターンまたは25パターンに分類し、同じ傾向の銘柄を探すことができるツールです。多くの銘柄の中から効率的に目的の銘柄を探すことができます。
例えば、SBI証券では下の図のようなツールを提供しています。
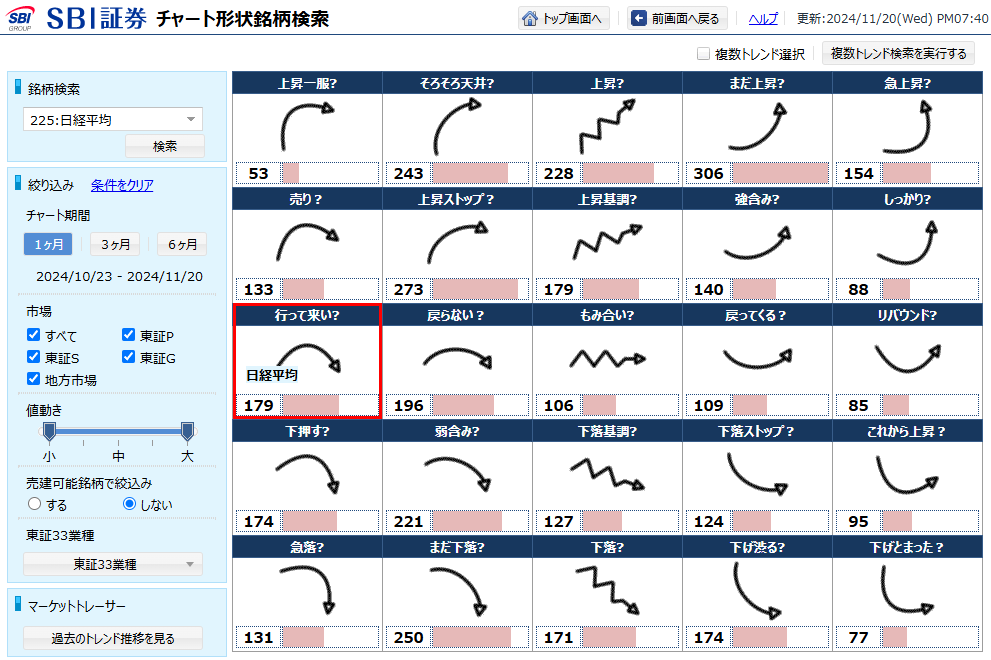
似たチャート形状の銘柄でスクリーニングされているので、チャート形状のパターンを選択することで、視覚的に上昇している銘柄や下降している銘柄を探すことができます。
相関係数とは
相関係数とは、2つのデータの間にある関係の強弱を測る指標です。-1から1までの値を取り、相関係数が1に近いほど正の相関、-1に近いほど負の相関、0に近いほど相関がないことを意味します。
つまり上記のような矢印の形状と株価の日足の形状を比較して、1に近いものを抽出します。
相関係数の注意点として、相関係数は関連の強さを示すものであり、因果関係を示すものではありません。
Pythonでチャート形状銘柄検索をする方法
今回は、SBI証券のチャート形状銘柄検索ツールの中の「急上昇?」、「上昇?」、「行って来い?」、「リバウンド?」、「下落?」、「急落?」の6個のチャート形状銘柄検索をしてみます。
証券コードのリストの用意
まずは、証券コードのリストを用意します。
おすすめの方法は、SBI証券の銘柄スクリーニングでCSVをダウンロードする方法です。
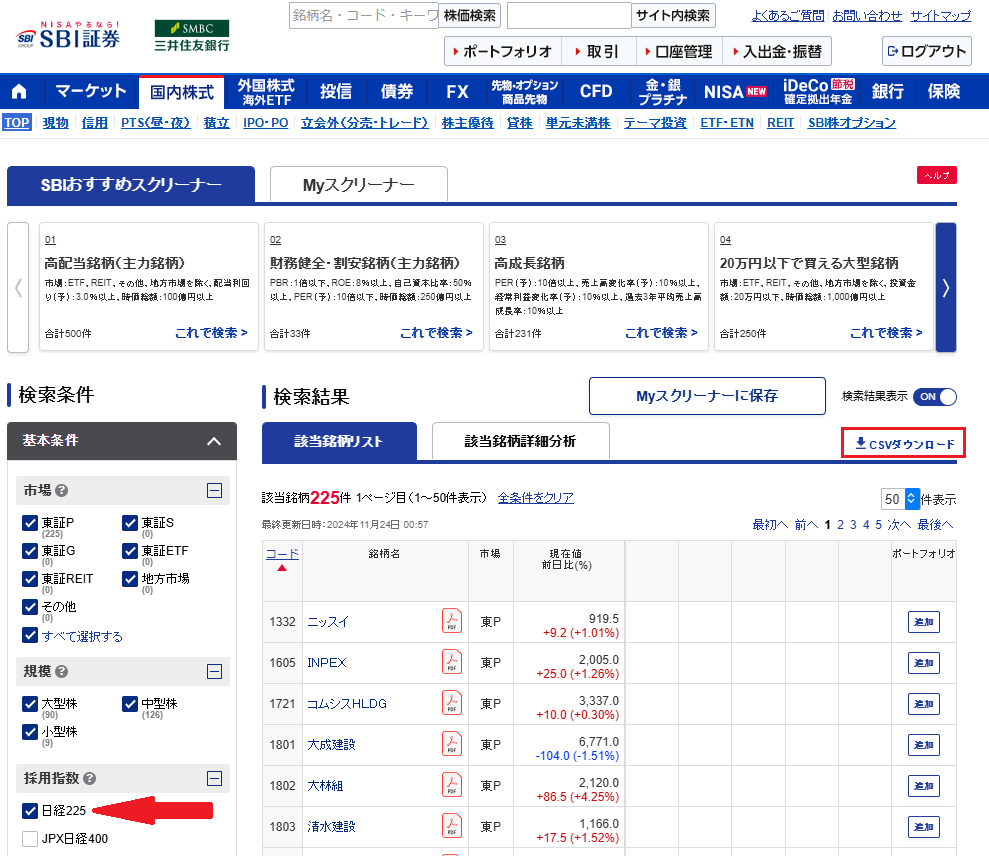
今回は日経225の銘柄からチャート形状検索をしたいと思うので、採用指数の日経225にチェックをします。
そして、CSVダウンロードをクリックするとscreener_result.csvというファイル名のデータが手に入ります。
ダウンロードしたscreener_result.csvをPythonの作業ディレクトリに移動させておきます。
ライブラリのインストール
今回は、以下のライブラリを使用します。pipでインストールしておいてください。
- numpy: 数値計算を効率的に行うためのライブラリ。
- pandas: 時系列データを処理するためのライブラリ。
- yfinance: 価格データを取得するためのライブラリ。
- mplfinance: グラフの描画に使用します。
pip install numpy pandas yfinance mplfinanceチャート形状銘柄検索をするサンプルコード
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
# 期間の設定 '1mo','3mo','6mo'から選択
period = '1mo'
# 株価を取得する関数
def get_data():
df = pd.DataFrame(columns=['code'])
csv_df = pd.read_csv('screener_result.csv', header=None, skiprows=1, usecols=[0, 1])
df['code'] = csv_df[0]
ticker_symbol_dr = []
for i in range(len(df)):
ticker_symbol_dr.append((str(df.iloc[i, 0])) + ".T")
symbol_data = yf.download(ticker_symbol_dr, period=period)
df = pd.DataFrame(symbol_data['Close'])
df = df.dropna(axis=1)
return df
# 相関係数を計算する関数
def calculate_correlation_coefficient(df, pattern):
for i in range(len(df.columns)):
a = df.iloc[:, i].tolist()
corr = np.corrcoef(a, pattern)[1, 0]
if corr > 0.8:
print(f"{df.columns[i]} 相関係数:{corr}")
data = get_data()
term = len(data)
# 株価データの正規化
normalization_df = (data - data.min(axis=0)) / (data.max(axis=0) - data.min(axis=0))
# X軸の正規化
x = list(map(lambda v: v / float(term - 1), range(0, term)))
# 各パターンの二次関数を計算
patterns = {
"急上昇": list(map(lambda v: (v / float(term - 1)) ** 5, range(0, term))),
"上昇": list(map(lambda v: v / float(term - 1), range(0, term))),
"行って来い": list(map(lambda v: -4 * ((v / float(term - 1) - 0.5) ** 2) + 1, range(0, term))),
"リバウンド": list(map(lambda v: 4 * ((v / float(term - 1)) - 0.5) ** 2, range(0, term))),
"下落": list(map(lambda v: -(v / float(term - 1)) + 1, range(0, term))),
"急落": list(map(lambda v: -(v / float(term - 1)) ** 5 + 1, range(0, term))),
}
for name, pattern in patterns.items():
print(name)
calculate_correlation_coefficient(normalization_df, pattern)
plt.plot(x, pattern)
plt.show()
これを実行すると、各パターンと相関関係が強い銘柄と比較対象となる二次関数のグラフが出力されます。
急上昇
2501.T 相関係数:0.9261513725403748
3382.T 相関係数:0.8741180629020509
5631.T 相関係数:0.8599507567993757
7453.T 相関係数:0.8416673868540776
8354.T 相関係数:0.8096845292616849
8411.T 相関係数:0.8478024340036924
8630.T 相関係数:0.8935440645929457
9021.T 相関係数:0.8000940138294604
9064.T 相関係数:0.9120862975283979
9432.T 相関係数:0.8390568047392546
9531.T 相関係数:0.8246114884778121ポイントの解説

株価データの取得
# 期間の設定 '1mo','3mo','6mo'から選択
period = '1mo'
# 株価を取得する関数
def get_data():
df = pd.DataFrame(columns=['code'])
csv_df = pd.read_csv('screener_result.csv', header=None, skiprows=1, usecols=[0, 1])
df['code'] = csv_df[0]
ticker_symbol_dr = []
for i in range(len(df)):
ticker_symbol_dr.append((str(df.iloc[i, 0])) + ".T")
symbol_data = yf.download(ticker_symbol_dr, period=period)
df = pd.DataFrame(symbol_data['Close'])
df = df.dropna(axis=1)
return df
まず、株価を取得する期間を設定します、1ヶ月、3ヶ月、6ヶ月から選択できます。
csv_df = pd.read_csv('screener_result.csv', header=None, skiprows=1, usecols=[0, 1])でSBI証券からダウンロードしたscreener_result.csvを読み込みます。
yfinanceで各銘柄の株価を取得する場合は、末尾に".T"が必要なので、ticker_symbol_dr.append((str(df.iloc[i, 0])) + ".T")で".T"を付け加えながらticker_symbol_drに加えています。
symbol_data = yf.download(ticker_symbol_dr, period=period, threads=False)で株価を取得して、df = pd.DataFrame(symbol_data['Close'])で終値のみを使用するようにしています。
また、欠損値がある場合はdf = df.dropna(axis=1)で除外します。
相関係数を計算
# 相関係数を計算する関数
def calculate_correlation_coefficient(df, pattern):
for i in range(len(df.columns)):
a = df.iloc[:, i].tolist()
corr = np.corrcoef(a, pattern)[1, 0]
if corr > 0.8:
print(f"{df.columns[i]} 相関係数:{corr}")
NumPyの相関係数を求めるnp.corrcoef関数で相関係数を求めます。
corr = np.corrcoef(a, pattern)[1, 0]で株価の終値と後述する二次関数との相関係数を求めて、0.8以上の銘柄を出力します。
正規化
# 株価データの正規化
normalization_df = (data - data.min(axis=0)) / (data.max(axis=0) - data.min(axis=0))
# X軸の正規化
x = list(map(lambda v: v / float(term - 1), range(0, term)))
正規化とは、データを一定の規則に基づいて変形し、比較や分析を容易にする処理のことです。
今回の場合はMin-Max正規化という手法で、各銘柄の最小値が0、最大値が1になるように株価の値を正規化します。
また、ラムダ式を用いて、二次関数で使用するX軸の正規化もします。
各パターンの二次関数を計算
# 各パターンの二次関数を計算
patterns = {
"急上昇": list(map(lambda v: (v / float(term - 1)) ** 5, range(0, term))),
"上昇": list(map(lambda v: v / float(term - 1), range(0, term))),
"行って来い": list(map(lambda v: -4 * ((v / float(term - 1) - 0.5) ** 2) + 1, range(0, term))),
"リバウンド": list(map(lambda v: 4 * ((v / float(term - 1)) - 0.5) ** 2, range(0, term))),
"下落": list(map(lambda v: -(v / float(term - 1)) + 1, range(0, term))),
"急落": list(map(lambda v: -(v / float(term - 1)) ** 5 + 1, range(0, term))),
}
ラムダ式で表記しているので分かりにくいかもしれませんが、各々次のような二次関数を表現しています。この二次関数の形状と株価の形状を比較します。
・急上昇?
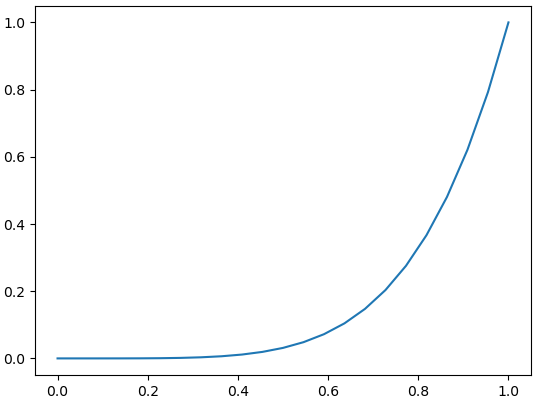
・上昇?
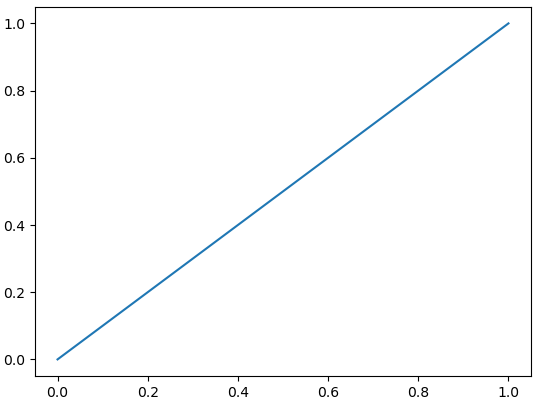
・行って来い?
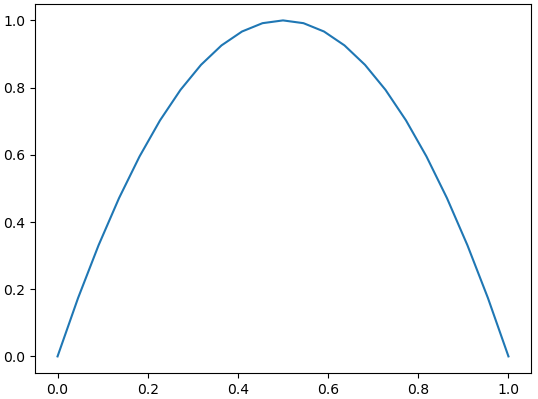
・リバウンド?
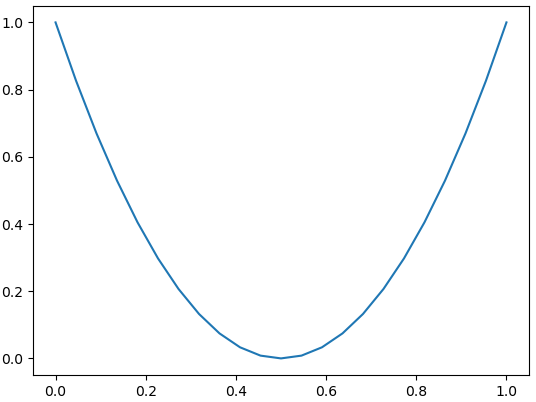
・下落?
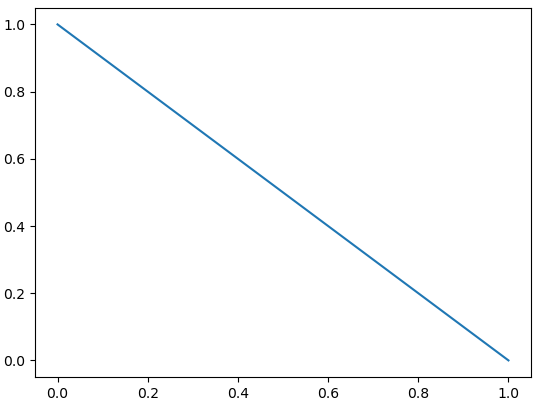
・急落?
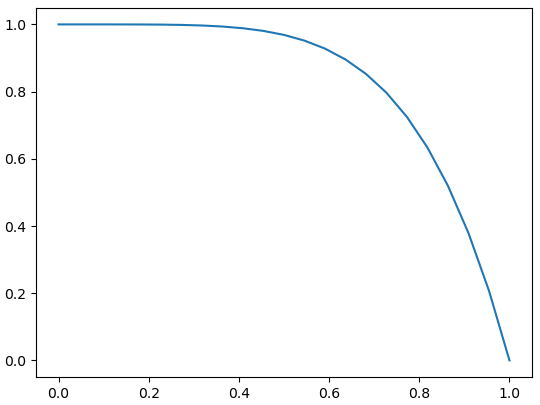
パターンの抽出
for name, pattern in patterns.items():
print(name)
calculate_correlation_coefficient(normalization_df, pattern)
plt.plot(x, pattern)
plt.show()
辞書オブジェクトの要素をfor文でループ処理するためにitems()メソッドを使います。
前述したcalculate_correlation_coefficient()関数で相関係数を計算します。
各パターンの二次関数のグラフを表示していますが、不要な場合はコメントアウトしてください。
おわりに
今回はチャート形状銘柄検索ツールの作成方法について解説しました。
相関係数を使うことで似ているチャートのパターンを抽出することができるので、大量にある銘柄の中から急上昇している銘柄などを見つけることが容易になります。
今回、使用したパターンは6種類でしたが、他のパターンについても挑戦してみてはどうでしょうか。


